I have a second story induced by Steve's brilliant talk and by people who don't do violence, but imagine violence. It's a story of a Viennese professor who is walking in front of his department and sees there's a flag of mourning over the department. Somebody says to him, "Oh, my God, that's so bad, one of your colleagues has died. Who is it?" And the professor said, "I don't know, I'm equally happy about anybody."
The title of my talk is "Evolution of Cooperation." I would like to begin at the beginning. This is a certain point, thirteen point seven billion years ago, which is the Big Bang. Here on this slide, I want to show you a few notable dates. I think there are very few dates that really are remarkable, and that we should know where great things have happened. Everything else is kind of small compared to these big, big things.
I asked my colleagues, the astrophysicists, when was the Big Bang? They tell me 13.7 billion years ago, and they have no doubt about it. They'll tell me three different ways of calculating that led exactly to this answer, so this is one of the firmest things we seem to know. Then, I ask an astrophysicist, when was the birth of our sun? He looks at me and says, "Four point five six seven billion years ago," with enormous precision. They even know the last super nova that occurred before this event, which gave rise to the heavy elements that are actually in us right now. That can be dated very precisely.
But now we come to biology and suddenly the precision of dating is no longer so accurate. Somehow we know there was an origin of life, but don't really know when the origin of life was. Interestingly, most scientists these days believe strongly that there was an origin of life on earth, as opposed to the possibility that earth was seeded by bacterial spores that have evolved on prior planets, material of which could have been in the molecular cluster that gave rise to the protoplanetary disk, which I think is another possibility. But this is not a possibility that the majority is entertaining. Most people believe there was a spontaneous origin of life on Earth maybe about four billion years ago.
The oldest number, which is debated, for the emergence of bacterial-based life is 3.8 billion years, but most people would rather be happy with 3.5 billion years. What we know about this date is actually not the fossil but the chemical evidence for bacterial-based life on Earth, that is what we have.
And then 1.8 billion. So for two billion years it was a planet of bacteria. At 1.8 billion years ago there were eukarya, higher cells, the cells that make up us, make up animals, plants, everything, so for two billion years it was a planet of bacteria. The way eukarya came about is by essentially an endosymbiotic fusion of bacterial cells. One bacterial cell made a living inside another bacterial cell, and that is believed to have given rise to the higher cells that contain a nucleus, organelles, and so on. The amazing thing is, it took two billion years for that to emerge. It's kind of strange because it seems a simple step compared to going from nothing at all to something as complicated as a bacterial cell.
The other thing that I find fascinating about this event is that you don't know what they made their living on. What was the advantage of these higher cells when they emerged?
Then 0.6 billion years ago, 600 million years ago, we have complex multicellularity. Complex multicellularity, as opposed to simple multicellularity (because simple multicellularity is probably as old as life itself), because bacteria can form filaments that are essentially multicellular animals, structures. The curious thing people have explained to me is that the problem with complex multicellularity is that the organism has an inside and an outside, and the inside has to get oxygen. You have to transport oxygen to the inside of the organism, which is complicated, whereas the simple multicellularity that evolved early on essentially has only an outside because they are not really big structures. That gave rise to animals, to fungi, to plants, basically everything, and that was 600 million years ago.
You could ask, what's the other interesting thing that happened in the last 600 million years? There's one other thing that recently I would put in here because of my collaboration with Ed Wilson. This is the evolution of insect societies, which he would put into this slide at about 120-150 million years ago, because insect societies, or social insects, gave rise to a huge biomass. Wilson talks about two social conquests of Earth: the one caused by insects and the other one caused by us.
The other thing that happened in the last 600 million years of true great evolutionary significance, was the evolution of what I call "I"-life, and that I would equate with human language. Why is human language really out there with the origin of life, with the emergence of cells, and multicellularity? Because, in my opinion, it gives rise to a new type of evolution.
Up to this point, evolution is mostly genetic evolution. But suddenly, we have evolutionary processes that are not dependent on genetic changes. One person has an idea, we don't have to wait for a gene to spread in the population to spread this idea. It is the idea that spreads, and what transmits the idea is language. Language is somehow allowing now for more or less an unlimited reproduction of information, and that really defines us. You could say humans invented a new form of evolution, and that defines our adaptability and our success, maybe for the good and for the bad.
Here's a completely boring slide about "the thinking path of Charles Darwin. " Here he walked up and down at his house in Kent, presumably thinking great thoughts about evolution.
Here's a very brief timeline known to all of you. Sir Charles Darwin was born 1809. At the same time there was the publication of Lamarck's book on evolution. When Darwin was a student in Edinburgh, evolution was the talk of the town. Everybody talked about evolution. People were fascinated by the idea of evolution, and the people who adhered to his idea of evolution were called Lamarckians.
Then, as you know, he had his voyage on the Beagle. In 1842, at the age of 33, he suddenly put his ideas together. At the age of 33, he was the first human person alive in history who looked at the world and had the idea that probably all life out there is related, and comes from one origin. I think that's a completely moving, mind-blowing and big idea, because Lamarck thought about changing species, but did not believe in a tree of evolution. Darwin had this idea of a tree of evolution.
What led Darwin to this idea was a number of confluent factors. One of them was from geologists. He learned that, given enough time, anything can happen. So, given enough time, mountains can actually be formed in very small steps. From animal breeders he got ideas on how to change aspects in animals, and from economists he got the idea that exponential population growth can actually lead to fierce competition and disaster. That led him to think that nature could be a big breeder, and what animal breeders are doing artificially, nature does actually. That gave rise to the idea of evolution, which he put down in this short essay.
Then what did he do with it? Nothing. He carried it around with him in his pocket because he made a calculation: "If I publish this, I lose all my friends." But then, interestingly, he gets this paper from Wallace, which I find another remarkable thing. There's this guy, Alfred Russell Wallace, who knows that Darwin is interested in this topic, and he writes a modern paper on evolution, and sends it to Darwin and asks him, "Please read it. If you think the idea is sound, would you be so kind to send it on my behalf to a journal?" It's very funny that he would send the crucial idea to his competitor and leave it in your competitor's hands. But it gave rise to the reading at the Linnean society, and in a certain sense, Darwin and Wallace as co-discovers of evolution. Wallace was also a great gentleman in the sense that he recognized that Darwin spent his whole life thinking about it, and he said, ‘I don't have to rush into publication. I will give you time to publish your book. I am happy to be the second.’ And then Darwin died.
There were two major objections to his theory that he didn't know how to answer. Some people list a third, which brings me to the topic of my talk, but really, the first two were the major objections.
The most important physicist of the time, Lord Kelvin, had calculated the age of the sun to be 200,000 years. Darwin didn't know what that meant for the evolutionary process because that doesn't seem to be a lot of time. Maybe that's enough time, but it didn't seem to be enough time. Nobody knew how to interpret that calculation.
The second objection I find even more interesting, and this was put forward by a British engineer. It's a mathematical argument. Essentially, Darwin believed in blending inheritance. So if you take height and then you have two parents, the offspring should have approximately the average height of the two parents. So if everybody blends with everybody else, after some time everybody has the same height and there is no variation anymore. If you have no variation, you have no selection anymore, so every evolutionary process must come to a dead end. He did not know how to answer this question, and the answer only became apparent with the development of the mathematical approach to a genetic understanding of evolution, which brought together Darwinian evolution, Gregor Mendel's genetics, and gives rise to the birth of population genetics.
A third, maybe minor objection, which Darwin wrote in one of his books, "If you find a trait in one species that is solely there to benefit another species, that would actually be an argument against my theory." I find this a very funny statement because when I look at the horse, it looks, to me, as if it's built for people to sit on. You could actually imagine that in the evolutionary process artificial selection is part of the evolutionary process also.
If there's just natural selection, if there's just fierce competition, how can we get any kind of cooperation, any kind of working together? So what is it that evolves? Populations evolve. What is evolution? In this beautiful book by Ernst Mayr, What Evolution Is, he points out very elegantly, loosely speaking, ‘we talk about the evolution of genes, the evolution of species, the evolution of the brain, but none of these things actually carry the evolutionary process. The only thing that really evolves are populations.’
What is it that evolves? Populations evolve, populations of reproducing individuals. That's the carrier of the evolutionary process. Mutation is just inaccurate reproduction. An error has happened and something new is now there. And selection means that there's a differential growth rate and one outcompetes the other.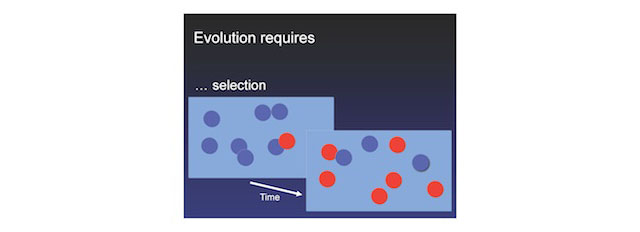
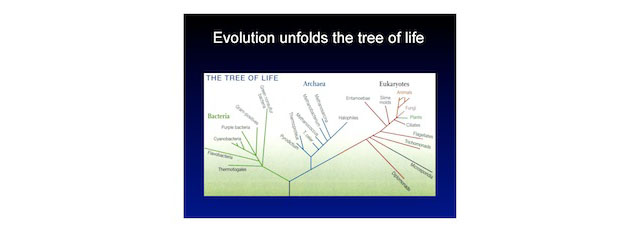
These are the fundamental ideas of evolution, and it's surprisingly simple. We are asked to believe that this very, very simple process is responsible for unfolding the tree of life. This is modern biology.
I want to point out one thing, however. If you step back and, for example, look at the mathematical approach to learning theory, people understand very well that there's a learning strategy, a search process, and there's a space that is being searched. Only the two together give you a mathematical description of learning. I would say the same is true for evolution. Evolution is the search strategy, but the space that is being searched is generated by the laws of physics and chemistry in a way that nobody actually understands. You could say that to really understand the structure of life around you, a much deeper description would actually be required, and would describe not the algorithm for search, but what is being searched. So, in that sense, our current understanding of evolution, I think, is actually very incomplete.
Now, cooperation: why is there great interest in cooperation? On one level, because it's in conflict with competition, so how can natural selection lead to cooperation? We'll get into this. But I'm fascinated by cooperation because it seems to be crucially involved in all the great creative steps of life that have happened. There's a point to be made that cooperation is needed for construction. Genomes you get when you have some kind of cooperation of genes to align themselves in genomes, to have sort of a shared fate. But cells are a cooperation of different kinds of genes that come together in the protocells and then the protocells have spontaneous divisions, and this is something I'm discussing with Jack Szostak, for example, at the moment, who in his lab evolves protocells with RNA and has spontaneous cell division.
It is therefore the emergence of multicellular organisms where the cells, for example in our body, don't just replicate like crazy, but they replicate when needed for the organism, which is a kind of cooperation. The breakdown of cooperation is when cells get mutations that revert back to the primitive program of self-replication. That would be cancer. So you could say cancer is a defector in this cooperative aggregate of the body.
You have cooperation in animal societies, like social insects, and you have cooperation in human societies. This is an image of traders that are aligned with some exchange, I don't know how much cooperation there is.
What is cooperation? Cooperation is a kind of working together in a game theoretic sense. It is an interaction of at least two people where there is a donor and there is a recipient, and the donor pays a cost and the recipient gets a benefit. Cost and benefit are measured in terms of fitness and reproduction, and can be genetic or cultural. We can apply it to the genetic process of evolution and to the cultural process of evolution.
The idea would be, I reduce my fitness to increase your fitness. The question is, "Why should I do this?", because natural selection should weed out this type of unselfish behavior. This interaction between two people leads to a famous game called the Prisoner's Dilemma. We have two people and both people have to make a choice between cooperation and defection. They have these two parameters that I just introduced, the cost of cooperation for you and the benefit for me, and vice versa. Here's a payoff matrix, and this payoff matrix shows what you will get if I cooperate, if you cooperate, if you defect, if I defect. The benefit is greater than the cost, which is greater than zero.
I would like to play this game with you, and I would like to ask you: who wants to cooperate with me, and who wants to defect? So who wants to cooperate? Who wants to defect? So, many people haven't decided. I should say this is not an optional game, because in an optional game there would be a third row: do nothing, and we also have this in game theory. But this is a compulsory game and people must choose between cooperation and defection. Normally, when I play this game in audiences, its about one third of the people who cooperate.
Here's one way to analyze this game; you don't know what I will do. Suppose I cooperate. Then you have a choice between "B minus C" and "B." So "B" is better than "B minus C." If I cooperate you actually want to defect. So here "zero" is greater than "B minus C," so if I defect you also want to defect. No matter what I might be doing, you want to defect. If I analyze the game in the same way, we both end up here and that is very unlucky because "B minus C" would have been positive, so we both have a low payoff. But if we had some way of having found cooperation, we would have both gained from it. Cooperation is better for both of us, but as an incentive for each one of us to switch to defection.
This is the rational analysis that is offered by game theorists and some of my students are offended when I present this in class because they don't want to be irrational and yet they want to cooperate. Most experiments show that people are not rational in that sense, and this is a particular notion of rationality that essentially you realize what is the Nash equilibrium and how to play the Nash equilibrium.
Two rational players defect and end up with a low payoff, and two irrational players might cooperate and receive a higher payoff.
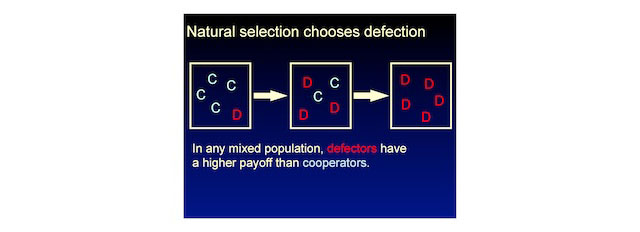
The interesting thing is, in natural selection evolutionary game theory you don't need the notion of rationality. We do the same analysis without rationality and we say here's a population of just cooperators and defectors, and they meet each other randomly, and they either cooperate or defect. You can quickly calculate that, no matter what, defectors always have a higher payoff. So, natural selection favors defectors until the population is just defectors.
Natural selection has here destroyed what would have been good for the population, because here the average fitness is high, lower, lowest. Natural selection here reduces the average fitness of the population, contrary to Fisher's fundamental theory that natural selection increases the average fitness of the population. This is a counter example, one of the counter examples noted by Fisher presumably, but his theorem isn't really formulated for these evolutionary games.
Natural selection needs help to favor cooperation over defection. This unselfish behavior truly is not favored by natural selection. We want to ask now, how can we help natural selection to favor cooperation over defection? What do we have to do? The way I propose to summarize the literature of many thousands of papers on precisely this question is, that there are five mechanisms.
There are five mechanisms for the evolution of cooperation, and a mechanism for me is an interaction structure, something that describes how the individuals in the population interact in terms of getting the payoff, and in terms of competing for reproduction. The mechanism is an interaction structure. The five mechanisms are: kin selection; direct reciprocity; indirect reciprocity; spatial selection; group selection. I want to give you a flavor of each of them in turn.
Kin selection is the idea that interaction occurs between genetic relatives. J. B. S. Haldane, one of the founding fathers of population genetics said, "I will jump into the river to save two brothers or eight cousins." He was not only a founding father of population genetics, but also politically very active, and here he is addressing a group of British workers. (He was a dedicated Communist, presumably here not talking about kin selection theory.) But this theory was made very, very famous in the Ph.D. thesis of William Hamilton, and Hamilton developed a mathematical approach to describe it.
The center of his approach is something called Hamilton's Rule. Hamilton's Rule says that kin selection can lead to the evolution of cooperation if relatedness is greater than the cost benefit ratio.
Recently, I've been very much involved in a controversy regarding the merits of the mathematical approach of inclusive fitness to actually help us to analyze such situations. (If you are interested in this, at the end of my talk, I can actually discuss this controversy.) But I have no problem with the importance of genetic relatedness, and I have no problem with the fact that kin selection is a mechanism for the evolution of cooperation if properly used in the sense based on kin recognition and conditional behavior, so I recognize my relative and I behave accordingly. The point that I'm making is that the inclusive fitness theory concept for analyzing such situations is misleading, flawed, or not really necessary. There is no need to evoke inclusive fitness in order to understand aspects in social evolution. That's the heart of the controversy.
The second mechanism is direct reciprocity: I help you and you help me. There was a very influential paper by Robert Trivers in 1971. Here you can see him visiting my institute a few years ago, here in 1971 sleeping surrounded by his books thinking about direct reciprocity, perhaps.
The idea now is that we meet each other again and again, and now I help you and then you might help me, and this is how we can actually get to cooperation.
We play the Repeated Prisoner's Dilemma repeatedly. Economists know for the Repeated Prisoner's Dilemma, the so-called folk theorem, which is if the game is repeated sufficiently often there is Nash equilibrium, there are equilibria with any level of cooperative outcome. So you can get cooperation if the game is sufficiently repeated.
But the folk theorem doesn't really tell you how to play the game. In the late '70s, Robert Axelrod asked precisely this question: what is a good strategy for playing this game? He said, let's have these computer tournaments. You send me strategies, and I will have them play against each other, and then we will see what's the winning strategy. The great surprise is he conducted two such computer tournaments and the simplest of all strategies submitted won. This was Tit-for-tat, a three-line computer program sent by Anatol Rapoport.
The three-line program works in the following way: I start with cooperation, and then I do whatever you did in the last round. So we play the repeated Prisoner’s Dilemma, I will always begin with cooperation and then just do what you do. Essentially I'm holding up a mirror and you are playing yourself. You may not notice. It was very surprising that this was the winning strategy. So they repeated such a competition where everybody knew the outcome, and people designed strategies to beat Tit-for-tat. Only Rapoport submitted Tit-for-tat again, and it won again. At that point it was the world champion of the repeated Prisoner's Dilemma.
But the world champion has an Achilles' heel. The Achilles' heel is, in Axelrod's tournament there were no mistakes. In the real world, there are mistakes. We can have bad days. Economists talk about trembling hand and fuzzy mind, and that leads to mistakes. So if one of the two Tit-for-tat makes a mistake, you retaliate, another mistake. On average, we get a very low payoff. We have to move out of this.
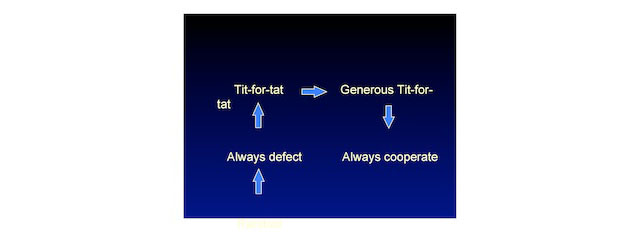
This is when I started to do my PhD thesis with Karl Sigmund in Vienna. What we wanted to do was to let natural selection design a strategy. Let's not ask people to submit strategies, let’s let natural selection search a space of strategies. In that space of strategies we start with random distribution and then what happened is that Always defect came up first. So if the opposition is disorganized, the best way is to screw them, is to defect. You have to defect. But then, fortunately for my PhD thesis, it's not over. Fortunately, you know, the following thing happened: Tit-for-tat suddenly came up, and Tit-for-tat we can prove mathematically has this property of being a very good catalyst for initiating the first move toward cooperation if everybody is a defector. It's a harsh retaliator. It can get a jumpstart for cooperation.
But what made my thesis really interesting was that within 20 generations, Tit-for-tat was gone. Tit-for-tat was replaced by a strategy that we called Generous Tit-for-tat, because we had errors. So Generous Tit-for-tat is the following thing: if you cooperate, I will cooperate, but if you defect, I will still cooperate with a certain probability. So my advice is, on the kitchen counter to have some dice, and when your partner defects you roll the dice and you decide whether to cooperate or defect, and this would save many marriages. It's a probabilistic strategy because if it's deterministic it could be exploited, but probability is hard to exploit and you can calculate the optimum level of forgiveness.
So what is very interesting is natural selection chooses a level of forgiveness. Or to put it another way, a winning strategy must be a strategy that is able to forgive. Without forgiveness you can't be a successful strategy in that game. So, we have an evolution of forgiveness, (and for that reason, a grant from the Templeton Foundation!)
We have now Generous Tit-for-tat, and what happened next was a surprise. I should have expected it but I didn't. With hindsight you can always expect it. It actually goes to always cooperate. If everybody here plays generous Tit-for-tat, and I play always cooperate, I'm a neutral mutant, I have no disadvantage. Random drift can lead to the takeover of the neutral mutant. Or, in other words, if birds go to an island where there are no predators, they lose their ability to fly. A biological trait, to be evolutionary stable, must be under selection. The retaliation, sometimes retaliation against defection goes out if nobody's trying to defect. So you've got to always cooperate by random drift. But if we'd always cooperate, now we can guess what happens next: we invite Always defect. You have oscillations here, you have a mathematical model of human history, of economic cycles, of ups and downs.
There is one thing that I have learned in my studies of cooperation over the last 20 years: there is no equilibrium. There is never a stable equilibrium. Cooperation is always being destroyed and has to be rebuilt. How much time you spend on average in a cooperative state depends on how quickly you can rebuild it. The most important aspect is really how quickly you can get away from the Always defect again.
There is another strategy that we discovered in an expanded study, which is Win-stay, lose-shift. Win-stay, lose-shift has advantages over "Tit-for-tat"-like strategies that are known by economists and game theorists but by very few other people. Win-stay, lose-shift works in the following way: I will change my choice if I'm doing badly, but I will keep my choice if I'm doing well. We can actually write down what that strategy does. It can also correct for mistakes. It does not have this instability with Always cooperate, and it can lead to a longer-lasting cooperative society.
The interesting thing is that the Repeated Prisoner's Dilemma for most people is a story of Tit-for-tat. But mathematicians who analyze this game know that Tit-for-tat has actual instabilities that these type of strategies do not have.
But here's another problem: most of this mathematical analysis is directed at simultaneous Prisoner's Dilemma. One can imagine an alternating Prisoner's Dilemma: you play and I play, you play, I play. For the alternating Prisoner's Dilemma, I have not found a win-stay, lose-shift strategy that does well. For the alternating Prisoner's Dilemma we might be back to generous "Tit-for-tat"-like strategies. I discussed this also with Drew Fudenberg and he pointed out to me that the reality is perhaps between simultaneous and alternating. The reality is never strictly alternating and never absolutely simultaneous. This was the second mechanism.
Now I come to my third mechanism, indirect reciprocity: I help you and somebody helps me. Here's the Vincent van Gogh painting of the Good Samaritan and whatever his motive was, presumably he did not think this is the first round in a Prisoner's Dilemma. In the first round one cooperates. I think many of our interactions work in this way: yes, I'm willing to help, I'm willing to cooperate, and yet I do not expect this to be a Repeated Prisoner's Dilemma. Or the university president goes to a donor and asks for a donation, presumably the donor does not think this is a Repeated Prisoner's Dilemma, and nevertheless, might be inclined to do it. How do we get this type of cooperation? My proposal is with Indirect reciprocity. I help you and that gives me the reputation of a helpful person, and then others help me. So if I don't help you my reputation decreases, if I do help you my reputation increases.
We know how this works from the way evaluations work on E-Bay. For example, you make a deal, you get a good evaluation, your value goes up. We have also played experimental games where people can purchase reputation, they can trade reputation if they have good reputation, so we can actually determine the price of a good reputation in experimental situations. This indirect reciprocity relies on gossip; some people might have an interaction and others observe it, and others talk about it. We are obsessed with gossip. We are obsessed with talking about others and how it would be to interact with them. In an experimental study, people go up and down in trains in Britain and listen to what people are talking about, to find that about 60 percent of the conversation topics fit into this general framework of indirect reciprocity.
What is very important for efficient indirect reciprocity is language. Indirect reciprocity leads to the evolution of social intelligence and human language. In order to evaluate the situation, you have to understand who does what to whom and why. And we have to have a way to talk about what happened, to gain experience from others.
As my friend David Haig at Harvard put it very nicely, "For direct reciprocity you need a face; for Indirect reciprocity you need a name." And I find this beautiful because there is a lot in a face. A lot can be read from facial features. A big part of our brain is there to recognize faces, so we can recognize with whom the interaction was, to play simultaneous repeated games. But for Indirect reciprocity that's not enough; we also need a name. And as much or as little as we know about animal communication, we don't have an example, I think, where animals could refer to each other with a name. That could be a particular property that came with human language. So this was the third mechanism, indirect reciprocity.
The next mechanism is spatial selection. Spatial selection is the idea that neighbors help each other. Neighbors form clusters, or you and your friends have many interactions and you cooperate, and you can even be an unconditional cooperator with your friends, and that can work out.
This is an evolutionary graph theory where you have a social network and people interact with others on the graph. More recently, we also developed more a powerful mathematical approach that we call evolutionary set theory, where you belong to certain sets, for example, the Mathematics Department, the Biology Department, Harvard, or MIT, or the gym, or the tennis club, and I interact with people in that set. I cooperate with the people in the set and I try to join sets of successful individuals. So the extension to classical evolutionary game theory here is in classic evolutionary game theory, people imitate successful strategies. Here they imitate successful strategies in successful locations. They want to move into successful locations, and that can give rise to this clustering that allows evolution of cooperation.
The last mechanism that I want to discuss is group selection. Here is a beautiful quote from Charles Darwin from his 1871 book, "There can be no doubt that the tribe including many members who are always ready to give aid to each other, and to sacrifice themselves for the common good, would be victorious over other tribes. And this would be natural selection." Imagine here competition between tribes, and in one there is self-sacrifice, and there is sacrifice for the others. He thinks that this would be victorious over other tribes, and he calls this natural selection.
Group selection has a long and troubled history, but mathematically you can make it very precise, you can make it work. Here's a simple example. You play the game with others in your group, the offspring are added to your group, groups divide when reaching a certain size, and groups die. Then you can calculate the condition for evolution of cooperation in this example. You can also add some migration between groups, and if there's too much migration it destroys the effect, but a certain level of migration tolerates the effect.
I have discussed five mechanisms for cooperation: kin selection: the idea is cooperation with genetic relatives; direct reciprocity: I help you, you help me; indirect reciprocity: I help you, somebody helps me; spatial selection: clusters of cooperators or neighbors to help each other; group selection: groups of cooperators out compete other groups.
For all these mechanisms there are simple formulas that describe some essential parts of this. For kin selection this would be the benefit-to-cost ratio. This can almost always be expressed as the benefit-to-cost ratio being greater than something, and the key parameter here is genetic relatedness, the probability of another round, the probability to know the reputation of someone. Here it is actually just as a simple function, (a sigma got in it so it got screwed up) but it is a structural coefficient. For group selection, the benefit-to-cost ratio has to be greater than something that involves the group size and the number of groups.
What I find very interesting in these games of conditional reciprocity, direct and indirect reciprocity, we can make the point that winning strategies have the following three properties: they must be generous, hopeful and forgiving.
Generous in the following sense: if I have a new interaction, now I realize (and this is I think where most people go wrong) that this is not a game where it's either the other person or me who is winning. Most of our interactions are not like a tennis game in the US Open where one person loses and one person goes to the next round. Most of our interactions are more like let us share the pie and I'm happy to get 49 percent, but the pie is not destroyed. I'm willing to make a deal, and sometimes I accept less than 50 percent. The worst outcome would be to have no deal at all. So in that sense, generous means I never try to get more than the other person. Tit-for-tat never wins in any single encounter; neither does Generous Tit-for-tat.
Hopeful is that if there is a new person coming, I start with cooperation. My first move has to be cooperation. If a strategy starts with defection, it's not a winning strategy.
And forgiving, in the sense that if the other person makes a mistake, there must be a mechanism to get over this and to reestablish cooperation.
This is analysis of just what is a winning strategy. This is not an analysis of what is a nice strategy, this is just an analysis of what is a winning strategy, and it has these properties.
Q & A
JARON LANIER: In machine learning and in modeling perception, there’s an interesting similarity of the function of noise to the function of the winning game strategies you’ve described. If you're trapped in a local minimum within in an energy landscape, you need some noise, a little bit of thermal energy, to pop you into to a potentially better one. There's a funny way in which this gives noise a moral quality. If you're going to project it into humanistic terms, it would translate into: Ioo much self-certainty is the enemy of all of these good cognitive qualities- and that’s even true mathematically.
An interesting problem is when we face a global challenge. Global warming is a great example, where the whole population would benefit from finding a degree of cooperation, but we're evolved to be in competing groups. When you start to have the global group facing an enemy that is not another group, but simply circumstance, that can confounds our most familiar strategies. I wonder if that's part of how mankind came to evolve imaginary foes, which we find in universally in religions and so forth. If we need to imagine some other entity that we're playing the game against in order to cooperate in a larger group than before.
MARTIN NOWAK: The first question was noise, and noise comes in in a kind of beneficial way, in different ways here. The one is the noise in the evolutionary process. The noise in which strategies reproduce from one generation to the next. This allows you to explore fitness landscapes, it allows you to avoid being stuck at a certain place. Another thing that avoids being stuck is sexual reproduction. Sexual reproduction is a kind of noise generator to generate combination …
JARON LANIER: That's been my experience…
MARTIN NOWAK: Another way noise comes in, interestingly, is in the repeated game. If you don't have noise, there's a lot of unbroken symmetry between strategies. Many strategies look the same because often equilibrium particulars are never visited without noise. So noise is something that differentiates the subtleties of strategies. Only adding noise to the analysis actually gives you the rich understanding.
The other thing that you mentioned, yes, I'm very grateful for those remarks. I have talked mostly in terms of interaction between two people, but the theory also includes the sort of public goods game. The public goods game is a Prisoner's Dilemma where multiple people play, so each one is now a choice between cooperation and defection, but we are all sitting around the table. This is called the Public goods game.
What is very interesting in the public goods game is here if we would play it here, in the beginning people would be very hopeful. Many people would cooperate, but then one person would try "Let me see what happens when I defect," and then this person has a bigger income than everybody else. Then the others are annoyed and want to pay back, but the only way to pay back is also to defect in this game. So over time, in the public goods game, you lose cooperation. In principle there would be an equilibrium when I say that I start to defect as soon as one person defects. It then would actually force everybody to cooperate with Nash equilibrium, but the problem is, this is not realized by people.
What you need to get cooperation in public goods game is the possibility of targeted interaction also. We have not only the public interaction, but afterwards, I can have a targeted interaction. In the targeted interaction I can go out and punish defectors, or I can go out and reward cooperators. The field loves punishment. But I'm going to stop thinking of punishment because punishment could also be directed against cooperators as preemptive strikes.
In many experimental setups, that's prevented, so they don't see that, because that's not possible. What we have done is we have taken the public goods game with cooperation punishment. Others have done this, and played in different parts of the world. What defines in the US and Western Europe is many people use punishment to punish defectors. But in Eastern Europe, in the Arab world, in essence, defectors punish cooperators, and this is called antisocial punishment.
In this antisocial punishment, the question is, what is the motive for the antisocial punishment? The one explanation would be it's a preemptive strike. I know they will punish me, so let me punish them first. The other possibility is, I distrust everybody who actually thinks he can cooperate with the system, who cooperates with the system is a fool and is the person who makes me look bad, and I should actually punish them.
We did that experiment in Romania recently where we gave people an option between cooperation and reward. In the US, reward works amazingly well. Reward leads to efficient cooperation. The reward that we gave was the following; we play the public goods game, and afterwards we can have bare base productive interaction. We can play repeated Prisoner's Dilemma, and that ends up being good for us in private, and in public. People who cooperate in public will also get his private deals.
In Romania, what we observed was that the public cooperation broke down. Nobody cooperated in public, but people still cooperated in private. They didn't link the two games. The people said, that makes so much sense, because people distrust that a public project could ever work, but I rely on private income.
JOHN TOOBY: I've always had a little trouble seeing how indirect reciprocity gets started. I was wondering if you have models where the competent players are all present but indirect reciprocity is not, whether mutants would take off? Because if I'm helping people who have helped other people, that seems to incur a dubious fitness detriment, and it seems to me that the range of parameters within which that would evolve state would be…
MARTIN NOWAK: That is a very good question and I can show it here, for example, in this slide here.
This would be for direct reciprocity, but the similar situation applies to indirect reciprocity with one added complication. Here, you have always defect, and then that cooperator is at a disadvantage, so there is natural selection against the first person who wants to cooperate. The interesting thing is, if you take this intensity of selection analysis, if you actually take here the situation of evolution in a finite population, and you introduce one cooperator in the population of just defectors, and you ask, what is the probability that this cooperator will give us the lineage that takes over? That can be greater than the comparison with the neutral mutant, because initially the cooperator is disfavored, but then it is largely favored. So over all, a cooperator can behave like an advantageous mutant. But this works in this stochastic setting. This does not work in the deterministic setting.
In the deterministic setting and in the kind of Nash equilibrium analysis, you need to make an argument that there's a cluster of them. So once you get a cluster, then they can jumpstart the situation. But in the finite stochastic evolutionary process, a single one can actually be an adventitious mutant.
In this indirect reciprocity, the added complication is with the social norm that is used by people to evaluate interactions between others. That social norm itself should be the product of evolution, and that's something that nobody has really described yet because that's usually a given in a group. We think that cooperating with somebody with a good reputation gives you a good reputation. Cooperating with somebody with bad reputation gives you a bad reputation. This kind of social norm also must evolve. And here the only argument that was made verbally would be a group that has a working social norm might be better than a group that doesn't a productive social norm.
JOHN TOOBY: Just to follow up, the models that you have, today has a present ongoing process of direct reciprocity. The ones I saw initially they excluded direct reciprocity.
MARTIN NOWAK: My first models excluded direct reciprocity, yes.
JOHN TOOBY: And subsequent ones have…
MARTIN NOWAK: No. Many models exclude direct reciprocity because the population, the same people don't meet, so the two, most of them exclude. But logically, for me, there is no reason to exclude direct reciprocity from indirect reciprocity. I would like to see the two together. But for me, indirect reciprocity is the add-on that I can benefit not only from my own experience with somebody, but from the experience of others.
STEWART BRAND: I wonder how much this applies in microbial evolution, which is sort of Lamarckian after all, acquired characters are passed on to offspring. It seems like a much noisier environment since the genes are flowing around in all directions at all times. They do quorum sensing, they make bio-forms, they do things like this, but is this a drastically less cooperative environment?
MARTIN NOWAK: I think there are many possibilities for cooperation in bacteria, and they are being researched intensively at the moment. One example that I've discussed with Jeff Gore at MIT, who has a group, is that there are bacteria that produce enzymes that digest in some food that is in the medium. So they produce the enzyme, the enzyme goes out of the cell and digests the food, and the digested food is available to all bacteria no matter whether they produce that enzyme or not. So there's a kind of cooperation that takes over.
However, it has the following ease into the situation that the enzyme, a large part of that enzyme, is stuck in the cell wall of the bacteria and acts directly there. So, by producing the enzyme you have directly an advantage, and you have this indirect effect. These two together can lead to the situation of evolution of cooperation. But the way I would see evolution of cooperation in bacteria is mostly with the spatial selection, because they form structures, they form clusters, and in this spatial scenario you can get evolution
STEWART BRAND: So in a sense the whole idea of reputation of continuity that you can rely on and iterate and so on, microbes don't do that.
MARTIN NOWAK: I think it is an open question. I think microbes could play conditional strategies. I could imagine that a microbe plays the following strategy: If I find enough, if I sense cooperation around me, I cooperate. If I don't sense cooperation around me, I don't cooperate. A conditional strategy is possible I believe also.
LEDA COSMIDES: I wanted to ask you, in this situation … in real life, there's an actual cognitive architecture there and any part of it can be tweaked, and so forth. In this situation are you providing which strategies could be mutated to which ones? Or are there free parameters? Are there novel architectures that can arise?
MARTIN NOWAK: What we have in the evolutionary analyses is that we give a strategy space, and in the strategy space we explore the evolution. But we would like to give a rather complete strategy space, so we would criticize evolutionary status where you limit a priori a strategy space. We would like to see some attempt for a complete strategy space. That's what we are doing.
LEDA COSMIDES: Right. But, for example, there are problems in real life about judgment under uncertainty. Am I in a repeated interaction, or am I not in a repeated interaction, and so forth. You can have regulatory variables, and you can have Bayesian updating, deciding based on cues about whether you are or not. Can that kind of thing evolve in the way that you're doing that or …
MARTIN NOWAK: This is not described in the simplest approach, but something that we have considered in subsequent approaches. Let's suppose people realize whether they are in a one-time situation or whether they are in a repeated situation, and they behave differently.
LEDA COSMIDES: Right.
MARTIN NOWAK: The strategy would depend on the perceived probability of another round.
LEDA COSMIDES: Yes, yes. Actually, we have a simulation that will come out on the 27th that's showing that you can get, if you have these internal regulatory versions, you can get sort of interesting things depending on whether you let the beliefs evolve, whether you let that given a correct belief, the disposition to cooperate of all. But it's sort of interesting because there are these parameters, the architecture that are allowed a freedom of all then … so that's why I was just wondering in what way that worked?
MARTIN NOWAK: So there's one new result we have; timing seems to be very important. You ask people to play a one-shot situation. If they decide quickly, they go for cooperation. If they take time to decide, they go for defection. If you force them to make a decision, to be quick, they are more cooperative. If you force them to think, they are more defection.
DANNY KAHNEMAN: Beware your first impulse, it’s the good one.
BEN CAREY: What about power? If I have more power than you, then I can defect and if we run these repeatedly it costs me nothing.
MARTIN NOWAK: This is something that I proposed recently to a graduate student actually. This is what I call unequal wealth.
BEN CAREY: Is there a system that holds up better than others when you have like large middle class or something like that?
MARTIN NOWAK: This is the way I see it at the moment without disturbing, it hasn't yet begun, but in the normal sense, everybody is equally wealthy and we accumulate payoff. Then I meet you and I see how much you made, and debate if I should perhaps switch to your strategy. We all have the same background fitness, and on this background fitness we add the income. So the new model: we start off with an unequal distribution background fitness, and now somebody starts off with a background fitness much higher than somebody else, maybe because income from other gains. In every round you know this person has a payout from his endowment, which is much higher than somebody else.
What it does is it reduces the intensity of selection. It actually goes precisely in this limit that I find the most interesting one. It makes the intensity of selection between cooperation/defection smaller, between the strategy choices smaller. If there's an a priori of unequal background, it makes it even harder for me to judge the source of your income.
JENNIFER JACQUET: I understand the definition of defector at the single shot level. How does the definition of a defector change, or does it?
MARTIN NOWAK: The one defective strategy would be … so a defective strategy in a repeated game would be one that, when playing with itself, or with others, switches to continuous defection.
JENNIFER JACQUET: In experiments they said they define it as somebody who cooperates less than average, so is that sort of …
MARTIN NOWAK: There would be levels of cooperation and defection that you could use, but we use the term like all out defectors, somebody that is like all D, always defect, or somebody who is like alternating between cooperation and defection. There would be a continuum.
NICHOLAS PRITZKER: What do you take from the social insects, ants for example? There's all this work in ant society.
MARTIN NOWAK: This is a long story. I started to talk to Ed Wilson about three years ago and it was fascinating. It was life transforming. I called his office and he tells me this is a headquarters, 11,000 species of ants that he has collected there, 400 of which he has discovered himself.
Then he tells me about leaf-cutter ants, one of his favorite ant species. They build underground structures that are as big as this room, and they grow fungi down there. They have soccer ball like big cavities in there where they grow their fungus. They go out to cut leaves, and he measured the size of the head you need to cut the leaf. Then they carry the leaf home and the little guy is sitting on top of the leaf to protect the big one against parasite attack. Then they dump the leaf in someplace and somebody else takes over the leaf and cuts it into smaller pieces. These smaller pieces are brought to somebody else to cut into smaller pieces. And then finally, the leaves are not what they eat, the leaves are what they feed their fungus and it's the product of the fungus that they actually eat. This whole city there are about three million animals but one queen, and the queen gives rise to all of them. All of them are offspring of the one queen.
The queen got mated in her life only in the virgin flight. In the virgin flight, this leaf-cutter queen gets mated with about ten or more males at a same time, and then she has to store the sperm that she gets in these matings throughout her whole life, which can be 15 years, because she never gets another sperm cell. So she has to keep all of the sperm cells alive inside her. Whenever she produces a male, she just lays an unfertilized egg. When she wants a female, she opens a pore and she uses one sperm to fertilize the egg and the fertilized egg is a female.
In her lifetime she can produce about 100 million offspring. When the queen dies the whole structure disappears within one year, even though it is extremely uNICHOLASnlikely that a single fertilized queen makes it, because the area is patrolled by other workers and they certainly want to kill a fertilized queen who wants to start a new colony. It's very unlikely for any queen to make it, but when the queen dies, the structure gets abandoned. They don't make a new queen even though the structure will disappear otherwise. It's impossible.
NICHOLAS PRITZKER: Is that true? I just read Wilson's novel.
MARTIN NOWAK: Anthill.
NICHOLAS PRITZKER: Right. The female, the female ants mind the queen until they realize the queen is dead and then they, in fact, go and try to start their own colony…
MARTIN NOWAK: This is possible for some. For some species, what they do is they start to lay unfertilized eggs, they produce males. But they don't get another queen to keep the colony going.
NICHOLAS PRITZKER: Create a new colony but they have to do it …
MARTIN NOWAK: But in the last year they could produce some males. But there are wasp species, social wasp studies by Raghavendra Gadagkarm whom I mentioned to you. He's this brilliant Indian naturalist who devoted his whole life studying one species of wasp. He's so much in love with this species that he studies another species only to understand that species better. Against all the advice he got in his early career to go to the US, he wanted to have a career in India. And he developed his whole career in India and he was elected a foreign member of the National Academy a few years ago, a great recognition.
In his wasp species, the following thing is happening: one fertilized queen, female, starts to build a nest. Other fertilized females come and they kind of fight it out. The two of them fight it out. Several outcomes are possible, but one outcome is that the one that came is willing to stay as a subordinate. And so only the first one will then lay all the eggs and the others that come help her to do this.
An interesting question is why would you want that? They are not genetically related in any degree. Why would they want to stay subordinate? The answer is, in some sense, the first queen could die and then they have a line of succession, and this is what we found out in his experiments. The animals know who is number one in line, and who is number two. And the way he found this out is he takes the nest and he cuts it in two, and he puts it together again, and now the queen can only dominate one half of it because she never comes to the other half. The queen actually, he also found this) produces a pheromone which rubs on the nest and if the smell is there, the others realize the queen is alive. But if she can't visit this other half of the nest, the others realize there's no queen, and so they can be queen. So there will be a successor.
Now he swaps the successor and the queen, and in 50 percent of cases the successor is accepted on the other side, and in 50 percent it's challenged on the other side. So, in 50 percent of cases this was number one; in 50 percent of cases this was number two.
STEVIN PINKER: You talked about this cycling among strategies as basically human history, but the way I understand it, these different phases, the entire society is dominated by always defectors, tit-for-tat-ers and so on. Which strikes me as quite implausible. What does strike me as quite plausible is that at any given time there's some state of equilibrium within a population of, say, psychopaths and saintly ascetics and probably the largest percentage of generous tit-for-tat-ers who keep track but also show a big generosity, probably some firm but fair people who stick by the rules.
Could this cycling it apply to stable equilibrium or even a shifting equilibrium within a population that has multiple strategies at any one time, where these four are represented in some stable ratio even if, perhaps, the actual lineages that adopt these strategies might shift over?
MARTIN NOWAK: The following thing happens. If we have just selection, and mutation is very, very, very small, then you might have these extreme cycles. Now, you add a little bit of mutation and you add more and more mutation and these cycles are there but they shift into the interior. So you do have cycles but they now contain populations of mixed strategies. If the mutation is very, very high, you can actually get a stable equilibrium in the middle.
STEVEN PINKER: Where you have a population of four discreet types, or four mixed strategies? Does each individual play one of those four?
MARTIN NOWAK: That depends on your strategy space that it would a priori. You can make it complicated if you said people blend mixed strategies and they mutate between mixed strategies.
STEVEN PINKER: You could also have, could it be fixtures of two levels mainly that the population contains different types, but the types themselves just pertain to the weighting that each individual gives to the probability of adopting either of those four strategies, what different individuals have in weightings?
MARTIN NOWAK: Yes, yes. It can get a bit complicated. You could say I have a strategy space, but any one person plays a distribution of the strategy space, perhaps a changing distribution of the strategy space, and then there is mutation that changes the distribution.
STEVEN PINKER: And different people have different weightings. That sounds an awful lot like life.
MARTIN NOWAK: But there were two fundamental natures kind of there on many different levels. Also in the final population size analysis, where you never have something here to say, we always do those oscillations. But if you make the mutation very large, you can force it into a boring interior equilibrium.
STEVEN PINKER: By mutation, does that also, in this case, include sexual recombination?
MARTIN NOWAK: If you like, the sexual production is also in there, yes, I guess so. I mean I've never done that in this type of model. But it leaves, for me, one of the big open questions, how to model mutation in the cultural sense? Because here, for me, this is where the analogy to genetic evolution and cultural evolution breaks down, because what exactly is a mutation in the cultural sense? It could be that I'm calculating what would be a best response to the existing strategy pool and come up with a new strategy.
STEVEN PINKER: That's why when people talk in psychology, they would say that the whole analogy between natural selection and cultural selection only goes so far, because the mutation is not random in the sense of being indifferent to the outcome. There really is intelligent design when it comes to the human brain and popular culture.
MARTIN NOWAK: In a real mathematical model of cultural evolution, you need to have to a better understanding of what exactly is a mutation.
STEVEN PINKER: Anyway, talking of psychology.
JARON LANIER: There's an extension to this kind of research that has become very worth exploring, just very recently. Suppose some of the parties operate computer networks used by some of the others, like say one of the parties in the game owns Facebook, or a hedge fund, or something like that. And suppose the players can only act in the game through networks that might be owned by other players. There's one kind of player, the network owner, who has privileged access to a lot of data about the others. Owners can run statistics and store correlations and over time can gain a better and better, and highly asymmetrical ability to predict behaviors of the other players. So if you have this sort of behavior prediction asymmetry, then the game becomes very interesting. Its not as if the network owners can automatically become the masters of the whole game, because they need to keep the other players using their network, and there is more than one privileged network. It's quite interesting.
It's a new frontier, so I wanted to suggest that if you know any graduate students who are looking for topics, this is worth thinking about.
My own sense, just from having done a little bit, is that owning a network can be similar to becoming a defector. Initially there are rewards but there are also long-term problems because the whole system can be degraded, depending on what you hope the system to do.
MARTIN NOWAK: I had some discussions with people in the world of finance that they would have been in strategy but it is the leading strategies longest, not too many others are imitating.
JARON LANIER: Right.
MARTIN NOWAK: If too many others imitate it, it starts to become a losing strategy.
NICHOLAS PRITZKER: Patent law. It's good for that.
JARON LANIER: That's true. Well, I think something like that's happened in finance in the last decade or so. Maybe there are some other examples that are out there as well, so if I change management is another one. Insurance is another one.
NICHOLAS PRITZKER: I'm kind of like cooperate, but keep a loaded gun under my belt. That'd be me. In other words, cooperate but watch your back. I find if you get away from simple A versus B you get to a situation where it's fine to cooperate but it pays to be cynical, you know, trust and verify, something like that. I find in the real world, for me, maybe outside of kinship relationships, or maybe even with, I have to really watch the nuance. You're not going to defect immediately but you want to keep your running shoes on.
MARTIN NOWAK: How do people really play these games of cooperation and defection? I think that we do try to cooperate a lot but it is not just that we play. We see this given set of strategies, we try to take actions to minimize our damage. If you would be exploited, it doesn't really have to hurt me that much. So, in some sense we immediately play around with the rules of the game. Here, the rules of the game are different and strategies are being adopted, but humans immediately mess around with the rules of the game, so we renegotiate the interaction for a slightly different payoff matrix, which may not be a Prisoner's Dilemma.
NICHOLAS PRITZKER: It would be interesting maybe to have experiments along these lines with children of various ages to look at cooperation versus defection, because I think a lot of us learn early on that if you trust other kids you're going to get messed with and you have to be very defensive.
MARTIN NOWAK: There's also one person in that group of experiments with kids and some of the interesting outcomes is that, the outcome depends on age, but one thing is that kids have the sense of fairness. They don't really like unfair deals even if they are to their own advantage, which I find actually surprising. So there's a stranger kid over there and the offer is for eight stickers for you and two stickers for the other, and the decision is rechecked, nobody gets anything, which I find strange because you deprive the other kid of two stickers, two candies.
STEVEN PINKER: That's after age seven, right? Age four they just care about whether it's unfair or not.
MARTIN NOWAK: It could be …
LEDA COSMIDES: Depends. Toshio Yamagishi has done stuff on this with preschoolers, and it also depends on whether they do or don't pass the false-belief test, which may be just about whether they can inhibit or not. But it's interesting because the younger ones will reject, in an ultimatum game, they will reject offers that they don't like. And both ages will offer a reasonable amount, but the ones that are passing the false-belief test are much less likely to reject a bad offer. He doesn't know exactly what that means except that he's worried that they're worried about what the adults will think.
JARON LANIER: I think it depends a lot on the kids…
LEDA COSMIDES: Also Asperger’s, people with Asperger's syndrome, they don't reject bad offers in the Ultimatum game, which is sort of interesting.
DANNY KAHNEMAN: The brain research indicates that the emotional side rejects, and the calculating side, the prefrontal areas, accepts those unfavorable offers.
LEDA COSMIDES: I had a Brazilian colleague who did the public goods game with nine year olds with chocolate, and there was a lot of chocolate stuffed in the pockets of the nine year olds. In these experiments there were a lot of attempts to not contribute to the public good.
Return to Edge Master Class 2011: The Science of Human Nature.
|
"We'd certainly be better off if everyone sampled the fabulous Edge symposium, which, like the best in science, is modest and daring all at once." — David Brooks, New York Times column
Future Science, edited by Max Brockman 18 original essays by the brightest young minds in science: Kevin P. Hand - Felix Warneken - William McEwan - Anthony Aguirre -Daniela Kaufer and Darlene Francis - Jon Kleinberg - Coren Apicella - Laurie R. Santos - Jennifer Jacquet - Kirsten Bomblies - Asif A. Ghazanfar - Naomi I. Eisenberger - Joshua Knobe - Fiery Cushman - Liane Young - Daniel Haun - Joan Y. Chiao "A fascinating and very readable summary of the latest thinking on human behaviour." — [More]
"Cool and thought-provoking material. ... so hip." — Washington Post The Best of Edge: The Mind, edited by John Brockman 18 conversations and essays on the brain, memory, personality and happiness: Steven Pinker - George Lakoff - Joseph LeDoux -Geoffrey Miller - Steven Rose - Frank Sulloway - V.S. Ramachandran - Nicholas Humphrey - Philip Zimbardo - Martin Seligman -Stanislas Dehaene - Simon Baron-Cohen - Robert Sapolsky - Alison Gopnik - David Lykken - Jonathan Haidt "For the past 15 years, literary-agent-turned-crusader-of-human-progress John Brockman has been a remarkable curator of curiosity, long before either "curator" or "curiosity" was a frivolously tossed around buzzword. His Edge.org has become an epicenter of bleeding-edge insight across science, technology and beyond, hosting conversations with some of our era's greatest thinkers (and, once a year, asking them some big questions). Last month marked the release of The Mind, the first volume in The Best of Edge Series, presenting eighteen provocative, landmark pieces—essays, interviews, transcribed talks—from the Edge archive. The anthology reads like a who's who ... across psychology, evolutionary biology, social science, technology, and more. And, perhaps equally interestingly, the tome—most of the materials in which are available for free online—is an implicit manifesto for the enduring power of books as curatorial capsules of ideas." "(A) treasure chest ... A coffer of cutting-edge contemporary thought, The Mind contains the building blocks of tomorrow's history book—whatever medium they may come in—and invites a provocative peer forward as we gaze back at some of the most defining ideas of our time." — [More] The Best of Edge: Culture, edited by John Brockman
17 conversations and essays on art, society, power and technology: Daniel C. Dennett - Jared Diamond - Denis Dutton - Brian Eno -Stewart Brand - George Dyson - David Gelernter - Karl Sigmund - Jaron Lanier - Nicholas A. Christakis - Douglas Rushkoff - Evgeny Morozov - Clay Shirky - W. Brian Arthur - W. Daniel Hillis - Richard Foreman - Frank Schirrmacher "We've already ravished The Mind -- the first in a series of anthologies by Edge.org editor John Brockman, curating 15 years' worth of the most provocative thinking on major facets of science, culture, and intellectual life. On its trails comes Culture: Leading Scientists Explore Societies, Art, Power, and Technology—a treasure chest of insight true to the promise of its title. From the origin and social purpose of art to how technology shapes civilization to the Internet as a force of democracy and despotism, the 17 pieces exude the kind of intellectual inquiry and cultural curiosity that give progress its wings. (A) lavish cerebral feast ... one of this year's most significant time-capsules of contemporary thought." —[More] |