2012 : WHAT IS YOUR FAVORITE DEEP, ELEGANT, OR BEAUTIFUL EXPLANATION?

Eratosthenes' measurement of the Earth's circumference

Eratosthenes (276-195 BCE), the head of the famous Library of Alexandria in Ptolemaic Egypt, made ground-breaking contributions to mathematics, astronomy, geography, and history. He also argued against dividing humankind into Greeks and 'Barbarians'. What he is remembered for however is having provided the first correct measurement of the circumference of the Earth (a story well told in Nicholas Nicastro's recent book, Circumference). How did he do it?

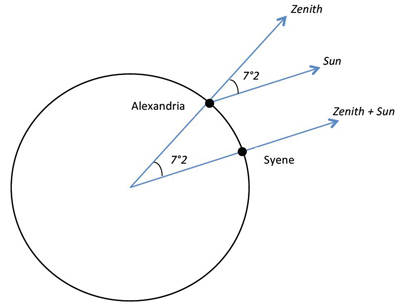
Eratosthenes had heard that, every year, on a single day at noon, the Sun shone directly to the bottom of an open well in the town of Syene (now Aswan). This meant that the Sun was then at the zenith. For that, Syene had to be on the Tropic of Cancer and the day had to be the Summer solstice (our June 21). He knew how long it took caravans to travel from Alexandria to Syene and, on that basis, estimated the distance between the two cities to be 5014 stades. He assumed that Syene was due south on the same meridian as Alexandria. Actually, in this he was slightly mistaken—Syene is somewhat to the east of Alexandria—, and also in assuming that Syene was right on the Tropic; but, serendipitously, the effect of these two mistakes cancelled one another. He understood that the Sun was far enough to treat as parallel its rays that reach the Earth. When the Sun was at the zenith in Syene, it had to be south of the zenith in the more northern Alexandria. By how much? He measured the length of the shadow cast by an obelisk located in front of the Library (says the story—or cast by some other, more convenient vertical object), and, even without trigonometry that had yet to be developed, he could determine that the Sun was at an angle of 7.2 degrees south of the zenith. That very angle, he understood, measured the curvature of the Earth between Alexandria and Syene (see the figure). Since 7.2 degrees is a fiftieth of 360 degrees, Eratosthenes could then, by multiplying the distance between Alexandria and Syene by 50, calculate the circumference of the Earth. The result, 252,000 stades, is 1% shy of the modern measurement of 40,008 km.

Eratosthenes brought together apparently unrelated pieces of evidence—the pace of caravans, the Sun shining to the bottom of a well, the length of the shadow of an obelisk—, assumptions—the sphericity of the Earth, its distance from the Sun—, and mathematical tools to measure a circumference that he could only imagine but neither see nor survey. His result is simple and compelling: the way he reached it epitomizes human intelligence at its best.

Was Eratosthenes thinking concretely about the circumference of the earth (in the way he might have been thinking concretely about the distance from the Library to the Palace in Alexandria)? I believe not. He was thinking rather about a challenge posed by the quite different estimates of the circumference of the Earth that had been offered by other scholars at the time. He was thinking about various mathematical principles and tools that could be brought to bear on the issue. He was thinking of the evidential use that could be made of sundry observations and reports. He was aiming at finding a clear and compelling solution, a convincing argument. In other terms, he was thinking about representations—theories, conjectures, reports—, and looking for a novel and insightful way to put them together. In doing so, he was inspired by others, and aiming at others. His intellectual feat only makes sense as a particularly remarkable link in a social-cultural chain of mental and public events. To me, it is a stunning illustration not just of human individual intelligence but also and above all of the powers of socially and culturally extended minds.